Ôn tập Toán Lớp 8 - Tuần 22+23, Tiết 43+44+45+46, Chuyên đề: Các trường hợp đồng dạng của tam giác

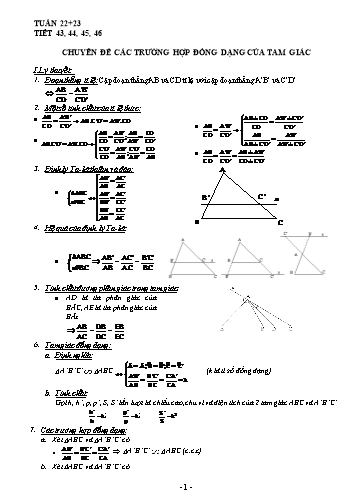
 TUẦN 22+23
TIẾT 43, 44, 45, 46
 CHUYÊN ĐỀ CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC
I.Lý thuyết:
1. Đoạn thẳng tỉ lệ: Cặp đoạn thẳng AB và CD tỉ lệ với cặp đoạn thẳng A’B’ và C’D’ 
 AB A'B'
 =
 CD C'D'
2. Một số tính chất của tỉ lệ thức:
 AB A'B' AB ± CD A'B' ± C'D'
• = AB.C'D' = A'B'.CD =
 CD C'D' AB A'B' CD C'D'
 • = 
 AB A'B' AB CD 
 = ; = CD C'D' AB A'B'
• CD C'D' A'B' C'D' =
 AB.C'D' = A'B'.CD AB ± C'D' A'B' ± C'D'
 C'D' A'B' C'D' CD
 = ; = AB A'B' AB ± A'B'
 • = =
 CD AB A'B' AB CD C'D' CD ± C'D'
3. Định lý Ta-lét thuận và đảo: A
 AB' AC'
 =
 AB AC
 • ΔABC AB' AC'
 = B' C' a
 a//BC BB' CC'
 BB' CC'
 =
 AB AC
 B C
4. Hệ quả của định lý Ta-lét
 ΔABC AB' AC' B'C'
 • = =
 a//BC AB AC BC
5. Tính chất đường phân giác trong tam giác:
 • AD là tia phân giác của 
 BÂC, AE là tia phân giác của 
 BÂx
 AB DB EB
 = = 
 AC DC EC
6. Tam giác đồng dạng:
 a. Định nghĩa: 
 Â = Â';Bµ = Bµ';Cµ = Cµ'
 A’B’C’ ABC A'B' B'C' C'A' (k là tỉ số đồng dạng)
 = = = k
 AB BC CA
 b. Tính chất: 
 Gọi h, h’, p, p’, S, S’ lần lượt là chiều cao, chu vi và diện tích của 2 tam giác ABC và A’B’C’ 
 h' p' S'
 k ; k ; k2
 h p S
7. Các trường hợp đồng dạng:
 a. Xét ABC và A’B’C’ cĩ: 
 A'B' B'C' C'A'
 • = = A’B’C’ ABC (c.c.c)
 AB BC CA
 b. Xét ABC và A’B’C’ cĩ: 
 - 1 - II.B ài tập: (trắc nghiệm) Chọn câu trả lời đúng nhất trong các câu sau đây:
Câu 1: Tỉ số của hai đoạn thẳng AB = 18 dm và CD = 12 cm là :
 2 3
 A. . ; B. . ; C. 15. ; D. 5.
 3 2
 1
Câu 2: Cho V ABC cĩ M AB và AM = AB, vẽ MN//BC, N AC .Biết MN = 2cm, 
 3
thì BC bằng:
 A. 6cm. ; B. 4cm. ; C. 8cm. ; D. 10cm.
 AB BC CA
Câu 3: Cho ABC MNP theo tỉ số đồng dạng k thì tỉ số là: 
 MN NP MP
 A. 3k. ; B. k2. ; C. k. ; D. 1 k.
 3
Câu 4: Cho V ABC cĩ AB = 5cm , AC = 6cm, đường phân giác AD, khi đĩ ta cĩ :
 BD 6 AB 6 DB 5 DC 5
 A. . ; B. . ; C. . ; D. .
 BC 11 AC 5 DC 6 DB 6
Câu 5: Độ dài x trong hình vẽ dưới là:
 A. 1,5. ; B. 2,9. ; C. 3,0. ; D. 3,2. 
 Câu 6: Trong hình biết MQ là tia phân giác N· MP
 x
 Tỷ số là: 
 y
 5 5 2 4
 A. . ; B. . ; C. . ; D. . 
 2 4 5 5
Câu 7: Độ dài x trong hình bên là: 
 A. 2,5. B. 3 .
 C. 2,9 . D. 3,2 . 
 .
Câu 8: Trong hình vẽ cho biết MM’ // NN’. 
Số đo của đoạn thẳng OM là: 
 A. 3 cm. ; B. 2,5 cm.
 C. 2 cm. ; D. 4 cm. 
 2
Câu 9: Cho ABC DEF theo tỉ số đồng dạng là thì DEF ABC theo tỉ số đồng dạng 
 3
là:
 2 3 4 4
 A. . B. . C. . D. .
 3 2 9 A 6
Câu 10. Độ dài x trong hình vẽ là: (DE // BC) 4 x
 A. 5. ; B. 6. D E
 2 3
 C. 7. ; D. 8.
 B C
 - 3 - Â = Dµ = 900 (gt) 
 a) vuơng ABC cĩ Bµ = 400 Cµ = 500 
 Cµ = F = 500 
 ABC : DEF (g-g) 
 b) vg ABC : vg DEF vì cĩ: 
 AB 6 3
 DE 4 2 AB BC
  
 BC 9 3 DE EF
 EF 6 2  
 -Bài 2: (49 trang 84 SGK)
 A 
 B H C
 GT : ABC; Â = 1v; 
 AHBC
 AB = 12,45cm
 AC = 20,50cm
 KL: a) Các cặp đồng dạng.
 b) Tính BC? AH? BH? 
 CH? 
 Giải : a) ABC ∾ HBA ( Bµ chung) 
 ∆ABC ∾ ∆HAC ( Cµ chung) ∆HBA∾ ∆HAC (cùng đd ABC)
 b) Trong tam giác vuơng ABC 
 BC2 = AB2 + AC2 (đl Pytago) 
 BC = AB2 AC2 12,452 20,502
 = 23,98 (cm) 
 ABC : HBA (cm trên) 
 AB AC BC 12,45 20,5 23,98
 hay 
HB HA BA HB HA 12,45
 HB = 12,452/23,98 6,46(cm)
 HA = (20,50.12,45):23,98 
 10,64 (cm) 
 HC = BC – BH = 23,98 – 6,46 
 17,52 (c/m)
 III.Bài tập đề nghị:
 -Bài 1: Cho hình bình hành ABCD. Gọi hình chiếu của A trên CD là H, hình chiếu của A 
 trên BC là K.
 Chứng minh: AHD : AKB
 - 5 - 2 2
 SEFGH 4 16(cm )
-Bài 4: HD: 
 A
 a/ AB2 + AC2 = BC2
Hay 4,52 + 62 =56,25 suy ra BC = 7,5cm 6
 4,5
 CAB : CDE (g.g) E
 EC DC
 BC AC
 B D 2 C
 BC.DC 7,5.2
 EC 2,5(cm)
 AC 6
 2 1 S 1 1
b/ k = CDE ( )2 
 6 3 SCAB 3 9
-Bài 5: HD: 
BC = 30cm( tính theo định lý Pitago) B
Tính BE
 BME : BAC ( chung Bµ )
 BE BM BC.BM 30.15
 BE 18,75(cm) M
 BC AB AB 24
Tính CD E
 BAC : DMC ( chung Cµ )
 BC AC BC.MC 30.15
 CD 25(cm)
 CD MC AC 18 D A C
V.Bài tập học sinh tự giải:
Bài 1:( cạnh huyền- cạnh gĩc vuơng)
 Cho hình thang vuơng ABCD( µA Dµ 900 ); AD = 17cm. Gọi E là một điểm trên cạnh 
AD. Biết BE = 10cm; EC = 15cm; DE = 9cm.
 a. Chứng minh : tam giác EAB đồng dạng tam giác CDE.
 b. Chứng minh : B· EC 900
-Bài 2:
 Cho tam giác A’B’C’ đồng dạng tam giác ABC cĩ chu vi lần lượt là 50cm, 60cm. 
Diện tích tam giác ABC lớn hơn diện tích tam giác A’B’C’ là 33cm.
 Tính diện tích của mỗi tam giác.
-Bài 3:
 25
 Cho tam giác A’B’C’ đồng dạng tam giác ABC. Biết S S và hiệu hai chu vi 
 A'B'C ' 49 ABC
của hai tam giác là 16cm. Tính chu vi của mỗi tam giác.
-Bài 4:
 Cho tam giác vuơng ABC( µA 900 ), đờng cao AH. Gọi I và K lần lượt là hình chiếu 
của H trên AB và AC.
a/ Tứ giác AIHK là hình gì ?
b/ So sánh ·AIK và ·ACB
c/ Chứng minh: AIK : ACB
d/ Tính SAIK biết BC = 10cm; AH = 4cm.
-Bài 5:
 - 7 -