Ôn tập Hình học 8 - Chủ đề: Tam giác đồng dạng (Tuần 22+23)

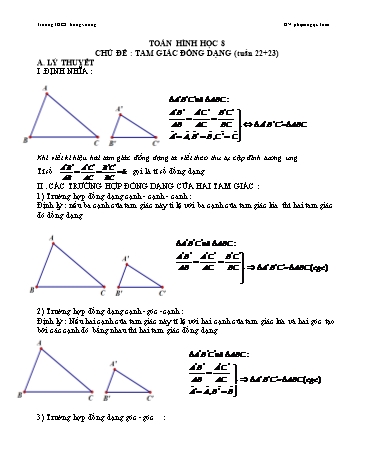
 Trường THCS hùng vương GV: phạm ngọc Tuấn 
 TOÁN HÌNH HỌC 8
 CHỦ ĐỀ : TAM GIÁC ĐỒNG DẠNG (tuần 22+23)
A. LÝ THUYẾT
I .ĐỊNH NHĨA :
 A B C và ABC :
 A B A C B C 
 AB AC BC  A' B'C'~ ABC
 Aˆ' Aˆ, Bˆ Bˆ,Cˆ' Cˆ 
Khi viết kí hiệu hai tam giác đồng dạng ta viết theo thứ tự cặp đỉnh tương ứng 
 A B A C B C 
Tỉ số k gọi là tỉ số đồng dạng 
 AB AC BC
II . CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA HAI TAM GIÁC :
1) Trường hợp đồng dạng cạnh - cạnh - canh :
Định lý : nếu ba cạnh của tam giác này ti lệ với ba cạnh của tam giác kia thì hai tam giác 
đó dồng dạng 
 A B C và ABC :
 A B A C B C 
 AB AC BC  A' B'C'~ ABC(cgc)
  
2) Trường hợp đồng dạng cạnh -góc -cạnh :
Định lý : Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kía và hai góc tạo 
bởi các cạnh đó bằng nhau thì hai tam giác đồng dạng
 A B C và ABC :
 A B A C 
 AB AC  A' B'C'~ ABC(cgc)
 Aˆ' Aˆ, Bˆ' Bˆ 
3) Trường hợp đồng dạng góc -góc : Trường THCS hùng vương GV: phạm ngọc Tuấn 
Bài 2 ) Cho hình thang vuông ABCD ( góc A = góc D = 900 ) có AB = 16cm , CD = 
25cm, BD = 20cm
a) C/m tam giác ABD đồng dạng tam giác BDC 
b) Tính BC 
Giải :
 ABD và BDC có :
 ˆ ˆ
 AB BD 16 20 b) ABD ~ BDC A DBC
 ( vì )
a) BD DC 20 25 mà Aˆ 900 nên DBˆC 900
 B1 D1 (slt ) theo ĐLpytagota có
 ABD ~ BDC(cgc) BC 2 CD2 BD 2 252 202 152
 BC 15
 1
Bài 3) Cho tam giac ABC có AB = 9cm, AC = 16cm,BC = 20cm . CMR : Bˆ Aˆ
 2
 A
 1 2
 B D C
Kẻ đường phân giác AD của tam giác ABC Trường THCS hùng vương GV: phạm ngọc Tuấn 
a) CM : tam giác HBA ~ tam giác ABC (gg)
 HB AB
 AB BC
 AB 2 HB.BC
b) Cm : tam giác HCA ~ tam giác ACB (gg)
 HC AC
 AC BC
 AC 2 HC.BC
c) C/m : tam giác HAB ~ tam giác HCA (gg)
 AH HB
 HC AH
 AH 2 HB.HC
C, BÀI TẬP TỰ LUYỆN
1) Cho tam giác ABC nhọn , đường cao và CE .
a) C/m: AD . AC = AE .AB
b) C/m: tam giác ADE đồng dạng tam giác ABC
c) Gọi H là giao điểm của BD và CE . C/m : BH . BD + CH . CE = BC2
2) Cho hcn ABCD , Vẽ AH vuông góc BD