Đề thi thử THPT Quốc gia nộp sở môn Toán - Năm học 2017-2018 - Trường THPT Trần Suyền (Có đáp án)

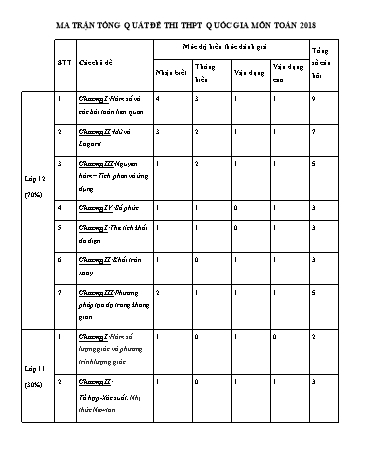
 MA TRẬN TỔNG QUÁT ĐỀ THI THPT QUỐC GIA MÔN TOÁN 2018 
 Mức độ kiến thức đánh giá
 Tổng 
 STT Các chủ đề số câu 
 Thông Vận dụng 
 Nhận biết Vận dụng hỏi
 hiểu cao
 1 Chương I:Hàm số và 4 3 1 1 9
 các bài toán liên quan
 2 Chương II:Mũ và 3 2 1 1 7
 Lôgarit 
 3 Chương III:Nguyên 1 2 1 1 5
Lớp 12 hàm – Tích phân và ứng 
 dụng
(70%)
 4 Chương IV:Số phức 1 1 0 1 3
 5 Chương I:Thể tích khối 1 1 0 1 3
 đa diện
 6 Chương II:Khối tròn 1 0 1 1 3
 xoay
 7 Chương III:Phương 2 1 1 1 5
 pháp tọa độ trong không 
 gian
 1 Chương I:Hàm số 1 0 1 0 2
 lượng giác và phương 
 trình lượng giác
Lớp 11
(30%) 2 Chương II: 1 0 1 1 3
 Tổ hợp-Xác suất. Nhị 
 thức Newton SỞ GD&ĐT PHÚ YÊN ĐỀ THI THỬ THPTQG NỘP SỞ, MÔN TOÁ N
 Trường THPT Trần Suyền Năm học: 2017-2018
 Tổ Toán Thời gian làm bài: 90 phút (50 câu trắc nghiệm)
ĐỀ CHÍNH THỨC:
Câu 1: Tı̀m tất cả các giá tri thực của tham số m để hàm số y mx sin x đồng biến trên R.
 A. m 1 B. m 1 C. m 1 D. m 1
Câu 2: Giá trị cực tiểu của hàm số y x3 3x2 9x 2 là:
 A. 20 B. 7C. 25 D. 3
Câu 3: Cho hàm số y f x có đồ thị như hình bên. Mênh đề ̣ 
nào dưới đây đúng?
A. Hàm số có giá trị cực tiểu bằng 2.
B. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 2 .
C. Hàm số đạt cực đại tại x 0và đạt cực tiểu tại x 2
D. Hàm số có ba cực trị.
 2
Câu 4: Hàm số y 4 x2 1 có giá trị lớn nhất trên đoạn  1;1 là:
A. 10B. 12 C. 14 D. 17
Câu 5: Tìm tất cả các giá trị thực của tham số m để phương trình x3 3x 2m 0 có ba nghiệm thực phân 
biệt. A. m 2;2 B. m 1;1 C. m ; 1  1; D. m 2; 
Câu 6: Tập hợp tất cả các giá trị thưc của tham số m để đường thẳng y 2x m cắt đồ thị của hàm số 
 x 1
y tại hai điểm phân biệt là:
 x 2
 A. ;5 2 6  5 2 6; B. ;5 2 6  5 2 6; 
 C. 5 2 3;5 2 3 D. ;5 2 3  5 2 3; 
Câu 7: Cho hàm số f x x3 3x2 2 có đồ 
thị là đường cong trong hình bên. Hỏi phương
 3 2
trình x3 3x2 2 3 x3 3x2 2 2 0 A. 0B. 1 C. 2 D. 3
 3 3 3
Câu 16 : Cho a,b,c là các số thực thuộc đoạn 1;2thỏa mãn log2 a log2 b log2 c 1. Khi biểu thức 
 3 3 3 a b c
P a b c 3 log2 a log2 b log2 c đạt giá trị lớn nhất thì giá trị của tổng a b c là:
 1
 A. 3 B. 3.2 3 3 C. 4 D. 6
 5 dx
Câu 17: Tính tích phân I = được kết quả I a ln3 bln5 . Giá trị a 2 ab 3b 2 là:
 1 x. 3x 1
 A. 4 B. 1 C. 0 D. 5
 2 3 
Câu 18: Tìm nguyên hàm của hàm số x 2 x dx
 x 
 x3 4 x3 4
 A. 3ln x x3 +C B. - 3ln x x3 C
 3 3 3 3
 x3 4 x3 4
 C. 3ln x x3 C D. 3ln x x3 C
 3 3 3 3
 2
Câu 19: Tính K = (2x 1) ln xdx
 1
 1 1 1
 A. K = 2ln 2 B. K C. K 2ln 2 D. K 2ln 2
 2 2 2
Câu 20: Diện tích hình phẳng giới hạn bởi đồ thị (C) của hàm số y 2x3 x2 x 5 và đồ thị (C’) của 
hàm số y x2 x 5 bằng
 A. 3 B. 1 C. 0 D. 2
Câu 21: Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = 2x – x2 và y = 0. Tính thể tích vật 
thể tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục Ox
 16 17 18 19 
 A. B. C. D. 
 15 15 15 15
Câu 22: Tìm số phức z thỏa mãn: 2 i 1 i z 4 2i
 A. z 1 3i B. z 1 3i C. z 1 3i D. z 1 3i
 2
Câu 23: Gọi z1, z2 là hai nghiệm phức của phương trình z 2z 10 0 . Tính giá trị của biểu thức 
 2 2
A | z1 | | z2 | . Câu 30 : Cho hình nón có góc ở đỉnh bằng 600 , diện tích xung quanh bằng 6 a2 . Tính thể tích V của khối 
 3 a3 2 a3 2
nón đã cho. A. V B. V C. V 3 a3 D. V a3
 4 4
Câu 31: Cho đường thẳng đi qua điểm M(2;0;-1) và có vectơ chỉ phương a (4; 6;2)
 Phương trình tham số của đường thẳng là:
 x 2 4t x 2 2t x 2 2t x 4 2t
 A. y 6t B. y 3t C. y 3t D. y 3t
 z 1 2t z 1 t z 1 t z 2 t
Câu 32: Mặt cầu (S) có tâm I(-1;2;1) và tiếp xúc với mặt phẳng (P): x 2y 2z 2 0 , phương trình là
 A. x 1 2 y 2 2 z 1 2 3 B. x 1 2 y 2 2 z 1 2 9
 C. x 1 2 y 2 2 z 1 2 3 D. x 1 2 y 2 2 z 1 2 9
Câu 33: Mặt phẳng chứa 2 điểm A(1;0;1) và B(-1;2;2) và song song với trục 0x có phương trình là:
 A. x + 2z – 3 = 0; B. y – 2z + 2 = 0; C. 2y – z + 1 = 0; D. x + y – z = 0
 x y 1 z 2
Câu 34: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : và mặt phẳng 
 1 2 3
 P : x 2y 2z 3 0 . Tìm tọa độ điểm M có tọa độ âm thuộc d sao cho khoảng cách từ M đến (P) 
bằng 2.
A. M 2; 3; 1 B. M 1; 3; 5 C. M 2; 5; 8 D. M 1; 5; 7 
Câu 35: Trong không gian Oxyz cho A(0; 1; 0), B(2; 2; 2), C(-2; 3; 1) và đuờng thẳng d : 
x 1 y 2 z 3
 Tìm điểm M thuộc d để thể tích tứ diện MABC bằng 3.
 2 1 2
 3 3 1 15 9 11 3 3 1 15 9 11 
A. M ; ; ; M ; ; B. M ; ; ; M ; ; 
 2 4 2 2 4 2 5 4 2 2 4 2 
 3 3 1 15 9 11 7 13 11 5 1 1
C. M ; ; ; M ; ; D.M( ; ; );M( ; ; ) 
 2 4 2 2 4 2 2 4 2 2 4 2
 2
Câu 36: Phương trình sin3x có nghiệm là: 
 2 
 k 
 A. x B. x k 
 4 n2 1 3 3n3 2
Câu 45: Giá trị của D lim bằng:
 4 2n4 n 2 n
 1 3 3
 A. B. C. D. 1 
 4 2 1
Câu 46: Trong các phép biến hình sau, phép nào không phải là phép dời hình ?
 A. Phép vị tự tâm O tỉ số 3 B. Phép vị tự tâm O tỉ số –1
 C. Phép đồng nhất D. Phép tịnh tiến. 
Câu 47: Trong mặt phẳng Oxy cho đường thẳng d có phương trình : 3x – 2y + 1 = 0. Ảnh của đường 
 thẳng d qua phép tịnh tiến theo véc tơ v = (1; 1) có phương trình :
 A. 3x + 2y + 4 = 0 B. 3x + 2y 1 = 0 
 C. 3x + 2y – 1 = 0 D. 3x – 2y 4 = 0
Câu 48: Cho hàm số y = cos32x . Đạo hàm của hàm số là y' bằng:
 A. - 3cos22x.sin2x. B. 3cos22x.sin2x. C. 6.cos22x.sin2x. D. - 6.cos22x.sin2x
Câu 49: Cho hình chóp ABCD. Gọi M, N, P lần lượt là các điểm trên AB, AC và BD sao cho
 AM AN
 (như hình vẽ ). 
 AB AC
 A
 M
 Đường thẳng MN cắt đường thẳng nào sau đây: 
 P
 B D
 A. Đường thẳng BC C. Đường thẳng CD N
 B. Đường thẳng BD D. Đường thẳng AD
 C
Câu 50. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. 
Gọi M, N lần lượt là trung điểm của SA và BC. Biết góc giữa MN và mặt phẳng (ABCD) bằng 600 . Khoảng 
cách giữa hai đường thẳng BC và DM là:
 15 30 15 15
 A. a B. a C. a D. a
 62 31 68 17
 -----------------HẾT-------------------- Vậy giá trị cực tiểu của hàm số là -25 tại x = 3
 Câu 3: Đáp án C
 Câu A sai vì giá trị cực tiểu của hàm số là -2 tại x = 2
 Câu B sai vì hàm số không có giá trị lớn nhất và nhỏ nhất mà chỉ có giá trị cực đại và cực tiểu
 Câu D sai vì hàm số chỉ có 2 cực trị là 0 và 2
 Câu 4: Đáp án D
 D = [-1;1]
 Ta có: y’= 4 x3 – 16x 
 => y’= 0  x = 0 (thỏa mãn) hoặc x = -2 (không thỏa mãn) hoặc x = 2 (không thỏa mãn)
x -1 0 1
y’ + 0 -
y
 17
 10 10
 Vậy giá trị lớn nhất của hàm trên đoạn [-1;1] là 17 tại x = 0
 Câu 5: Đáp án B
 Xét y = x3 3x
 Ta có: y’= 3x2 3 x 4 6 4 6 
 2 2
y’ - 0 + 0 -
y 5 2 6
 5 2 6 
 x 1
Vậy đường y = m cắt đồ thị hàm số y 2x tại 2 điểm phân biệt
 x 2
 m ( ;5 2 6)  (5 2 6; )
Câu 7: Đáp án là A
Ta có phương trình : 
(f(x))3 3(f(x))2 2 0
 f (x) 1 3 ( 2;2)
 f (x) 1 3 2
 f (x) 1 ( 2;2)
Số nghiệm của phương trình ban đầu là số giao điểm của ba đường thẳng y= 1 3 , y= 1 3 , y=1với 
đồ thị hàm số f(x)
=>y= 1 3 cắt đồ thị hàm số f(x) tại 3 điểm
y= 1 3 cắt đồ thị hàm số f(x) tại 1 điểm
y=1 cắt đồ thị hàm số f(x) tại 3 điểm
vậy có 7 nghiệm
Câu 8: Đáp án là C
Ta có: