Đề thi thử THPT Quốc gia năm 2020 môn Toán - Trường THPT Phan Chu Trinh (Có đáp án)

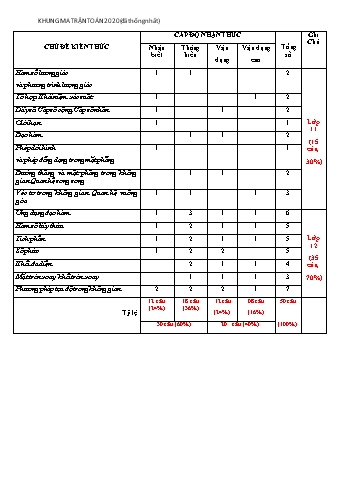
 KHUNG MA TRẬN TOÁN 2020(đã thống nhất)
 CẤP ĐỘ NHẬN THỨC Ghi 
 Chú
 CHỦ ĐỀ KIẾN THỨC Nhận Thông Vận Vận dụng Tổng 
 biết hiểu số
 dụng cao
Hàm số lương giác 1 1 2
và phương trình lượng giác
Tổ hợp. Khái niệm xác suất 1 1 2
Dãy số. Cấp số cộng. Cấp số nhân 1 1 2
Giới hạn 1 1 Lớp 
 11
Đạo hàm 1 1 2
 (15 
Phép dời hình 1 1 câu,
và phép đồng dạng trong mặt phẳng 30%)
Đường thẳng và mặt phẳng trong không 1 1 2
gian. Quan hệ song song
Véc tơ trong không gian. Quan hệ vuông 1 1 1 3
góc.
Ứng dụng đạo hàm 1 3 1 1 6
Hàm số lũy thừa 1 2 1 1 5
Tích phân 1 2 1 1 5 Lớp 
 12
Số phức 1 2 2 5
 (35 
Khối đa diện 2 1 1 4 câu,
Mặt tròn xoay, khối tròn xoay 1 1 1 3 70%)
Phương pháp tọa độ trong không gian 2 2 2 1 7
 12 câu 18 câu 12 câu 08 câu 50 câu
 (24%) (36%)
 Tỷ lệ (24%) (16%)
 30 câu (60%) 20 câu (40%) (100%) 3 3
 và 2 f x g x dx 6 . Tính f x g x dx .
 1 1
 A.7.B.6.C.8.D.9.
 2 1 1 
 Câu 14: (TH)Cho dx aln 2 bln 3 với a,b là các số nguyên. Mệnh đề nào dưới đây 
 1 x 1 x 2 
 đúng?
 A. a 2b 0 .B. a b 2 .C. a 2b 0 .D. a b 1.
Câu 15: (TH) Nghiệm dương bé nhất của phương trình : 2sin2 x 5sin x 3 0 là 
 3 5 
 A. x .B. .C. . x D. . x x 
 6 2 2 6
Câu 16:(TH) Tính đạo hàm của hàm số y log2 2x 1 .
 1 2 2 1
 A. y .B. y . C. y .D. y .
 2x 1 ln 2 2x 1 ln 2 2x 1 2x 1
Câu 17: (TH)Giá trị lớn nhất của hàm số y x2 2x 10 trên đoạn  1;4 bằng
 A. 11 . B. 7 . C. 2 . D. 13 .
Câu 18: (TH)Cho hàm số y f x có bảng biến thiên (hình 
 bên).Số nghiệm của phương trình 5 f x 2 0 là
 A. 3 . B. 2 .
 C. 1. D. 0 .
 2
Câu 19: (TH) Số giao điểm của đường cong y x3 x2 1 và 
 3
 đường thẳng y 4x 3 là
 A. 1. B. 2 . C. 0 . D. 3 .
 3
 Câu 20:(TH) Tìm tập xác định D của hàm số y x2 x 2 .
 A. D R \ 1;2 B. D 0; C. D ; 1  2; D. D R.
 Câu 21:(TH) Tìm tất cả các giá trị thực của tham số m để hàm số y ln(x2 2x m 1) có tập xác 
 định là R .
 A. m 0 .B. 0 m 3. C. m 1 hoặc m 0 .D. m 0 .
Câu 22: (TH) . Tìm số phức z thoả mãn z 2 z 11 3i .
 A . z 1 3i ; z 2 3i . B. z 1 3i; z 2 3i . C. z 1 3i; z 2 3i . D. z 1 3i; z 2 3i .
Câu 23: (TH) Tìm môđun của số phức z biết z 4 1 i z 4 3z i. 
 1
 A. z 4 . B. z 1.C. z .D. z 2 .
 2
Câu 24: (TH) Cho tứ diện ABCD, M, N lần lượt là trung điểm AC; CD. Mệnh đề nào dưới đây đúng?
 A. Hai đường thẳng MN và BC song song .B. Hai đường thẳng MN và AB cắt nhau.
 C. Hai đường thẳng MN và BC cắt nhau.D. Hai đường thẳng MN và BC chéo nhau.
Câu 25: (TH): Cho hình chóp S.ABC đáy là tam giác vuông tại B, SA vuông góc đáy. Mặt phẳng nào sau đây 
 vuông góc với BC?
 A. (SBC). B. (SAB). C. (ABC). D. (SAC).
Câu 26: (TH) Thể tích của khối chóp tứ giác đều có tất cả các cạnh bằng 2a là
 2 3 2 3
 A. a3 . B. a3 . C. a3 . D. a3 .
 6 6 2 2 Câu 38: (VD) Cho hình chóp S.ABCD đáy là hình chữ nhật, SA  (ABCD) , AB=a, AD=2a. Góc giữa (SCD) 
 và (ABCD) bằng 450 . Tính d(G;(SCD)) với G là trọng tâm tam giác ABC? 
 2 2 3 2 3 5 2 3
 A. a . B. a . C. a . D. a
 3 2 7 5
Câu 39: (VD) Cho hình chóp S.ABCD có tất cả các cạnh bằng a, M là trung điểm SB, (P) là mặt phẳng qua M 
 song song với mặt phẳng (SCD). Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (P)?
 3 3 3 2 2 3 2 5
 A. a2 . B. a2 . C. a2 . D. a2
 16 14 15 15
Câu 40: (VD) Cho hình chóp S.ABC có các mặt ABC và SBC là tam giác vuông cân tại B, AB 2a . Tính thể 
 tích khối nón đỉnh B, đáy là đường tròn ngoại tiếp SAC?
 4 6 3 6 4 3 4 3
 A. a3 . B. a3 . C. a3 . D. a3 .
 27 26 27 25
Câu 41:(VD) Cho mặt cầu (S): x2 y2 z2 1 0 và mặt phẳng (P): 2x y z 1 0 . Biết (S) cắt (P) theo giao 
 tuyến là đường tròn tâm H(a;b;c) .Tính a+b+c
 1 1 2
 A. . B. 0. C. . D. .
 3 2 3
 x y 2 z 1 x 1 y z 1
Câu 42:(VD) Trong không gian với hệ trục Oxyz cho d : và d : . Đường thẳng 
 1 1 2 3 2 2 3 1
 d vuông góc với mặt phẳng Oxz cắt d1;d2 lần lượt tại A và B. Tọa độ trung điểm AB là
 7 7 7 7 
 A. 1; ; 2 . B. 1; ; 3 . C. 1; ; 2 . D. 3; ; 2 . 
 2 2 2 2 
Câu 43:(VDC) Cho lăng trụ ABC.A’B’C’ có tất cả các cạnh bằng 3, ·A' AC ·A' AB 600 . Khoảng cách giữa AB 
 và CC’ bằng
 6 6
 A. . B. 2 6 . C. 6 . D. .
 3 2
Câu 44:(VDC) Cho hình chóp S.ABC, G, E, F lần lượt là trọng tâm SAB, SBC, SAC . Mặt phẳng (GEF) chia 
 V1
 khối chóp thành hai khối có thể tích V1,V2 (V1 V2 ) . Tính tỉ số 
 V2
 V 8 V 2 V 7 V 4
 A. 1 . B. 1 . C. 1 . D. 1 
 V2 19 V2 3 V2 15 V2 13
Câu 45:(VDC) Cho hình chóp S. ABC đáy là tam giác vuông cân tại B, AB=2a. Tam giác SAB đều và nằm trong 
 mặt phẳng vuông góc đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S. ABC.
 13 3 15 3
 A. a . B. a . C. a . D. a .
 3 3 4 8
 x 3 y 2 z
Câu 46:(VDC) Trong không gian Oxyz cho A(1;2;3), B(0;2;3), và đường thẳng d: . Viết phương 
 1 2 1
 trình đường thẳng d’ đi qua A cắt d và cách B một khoảng lớn nhất?
 x 1 x 1 x 1 t x 1 t
 A. y 2 4t . B. y 2 t . C. y 2 3t . D. y 2 3t .
 z 3 5t z 3 2t z 3 2t z 3 2t
Câu 47:( VDC) Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng abcd , trong 
 đó 1 a b c d 9 . 
 A. 0,079. B. 0,055.C. 0,014.D. 0,0495. HƯỚNG DẪN GIẢI 
Câu 23: (TH) Tìm môđun của số phức z biết z 4 1 i z 4 3z i. 
 1
 A. z 4 . B. z 1.C. z .D. z 2.
 2
Giải : 
 2 2
 PT z 1 3i z 4 i z 4 1 3i z z 4 z 4 
 2 2
 10 z 2 z 4 z 4 z 2 4 z 2. 
Câu 31: (VD) Trong một hình tròn bán kính R ,vẽ nội tiếp một hình vuông ,trong hình vuông đó vẽ nội tiếp 
một hình tròn ,trong hình tròn này lại vẽ nội tiếp hình vuông thứ hai và tiếp tục như vậy đến vô hạn .Gọi S là 
tổng tất cả diện tích các hình tròn ,giá trị S là
 4 3
 A. 2 R2 . B. R2 .C. R2 .D R2 .
 3 2
 Giải:
 2
Diện tích hình tròn thứ nhất bằng S1 R 
Cạnh hình vuông nội tiếp hình tròn thứ nhất bằng R 2 và bằng đường kính của hình tròn thứ hai , nên diện 
 2
 R 2 1
tích hình tròn thứ hai bằng S R2 .
 2 
 2 2
 1 1
Lập luận tương tự ,diện tích “tất cả” các hình tròn lần lượt là S R2 , S R2 , S R2 ,,
 1 2 2 3 22
 1 1
 S R2 ,Chúng lập thành cấp số nhân vô hạn ,lùi .Số hạng đầu S R2 ,công bội q .
 n 2n 1 1 2
 S
Vậy S S S ... S ... lim(S +S +...+S ) 1 2 R2 .
 1 2 n 1 2 n 1 q
 3
Câu 32. (VD) Cho các hàm số y f (x), y f f (x) , y f (x 2) có đồ thị lần lượt là (C1), (C2 ), (C3). 
Đường thẳng x 2cắt (C1), (C2 ), (C3) lần lượt tại A, B, C . Biết phương trình tiếp tuyến của (C1) tại A và 
của (C2 ) tại B lần lượt là y 3x 4 và y 6x 13. Lập phương trình tiếp tuyến của (C3) tại C .
 A. y 24x 49. B. y 10x 21. C. y 12x 49. D. y 2x 5.
Giải :
Các điểm A, B, C có hoành độ x 2 .
Phương trình tiếp tuyến của đồ thị hàm số y f (x) (C1) tại A có dạng:
 y f '(2)(x 2) f (2)
 f '(2).x 2 f '(2) f (2) 3x 4
 f '(2) 3 f '(2) 3
Đồng nhất 2 vế ta được: 
 2 f '(2) f (2) 4 f (2) 10
Tương tự ta có phương trình tiếp tuyến của đồ thị hàm số y f ( f (x)) (C2 ) tại B có dạng:
 y  f ( f (2))'(x 2) f ( f (2)) (C2 )
 y f '(2). f '( f (2))(x 2) f ( f (2))
 y 3. f '(10).x 6 f '(10) f (10) 6x 13
 f '(10) 2
 f (10) 1
 3 3 2 3
Hàm số y f (x 2) có đạo hàm y ' f (x 2) ' 3x . f '(x 2)