Đề thi thử THPT Quốc gia môn Toán - Năm học 2017-2018 - Trường THPT Phan Bội Châu (Có đáp án)

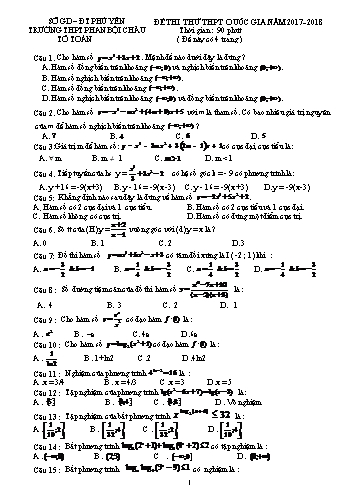
 SỞ GD – ĐT PHÚ YÊN ĐỀ THI THỬ THPT QUỐC GIA NĂM 2017- 2018
TRƯỜNG THPT PHAN BỘI CHÂU Thời gian : 90 phút
 TỔ TOÁN ( Đề này có 4 trang )
 Câu 1. Cho hàm số y x3 3x 2 . Mệnh đề nào dưới đây là đúng ?
 A. Hàm số đồng biến trên khoảng ( ;0) và nghịch biến trên khoảng (0; ) .
 B. Hàm số nghịch biến trên khoảng ( ; ) .
 C. Hàm số đồng biến trên khoảng ( ; ) .
 D. Hàm số nghịch biến trên khoảng ( ;0) và đồng biến trên khoảng (0; ) .
 Câu 2. Cho hàm số y x3 mx2 (4m 9)x 5 với m là tham số. Có bao nhiêu giá trị nguyên
 của m để hàm số nghịch biến trên khoảng ( ; ) ?
 A. 7 B. 4 C. 6 D. 5
 Câu 3:Giá trị m để hàm số: y = x 3 - 3mx2 + 3(2m - 1)x + 1 có cực đại, cực tiểu là:
 A. m B. m 1 C. m 1 D. m < 1
 x3
 Câu 4. Tiếp tuyến của hs y = 3x2 2 có hệ số góc k = - 9 có phương trình là:
 3
 A. y + 16 = -9(x+3) B. y - 16 = -9(x -3) C. y - 16 = -9(x +3) D. y = -9(x -3) 
 Câu 5: Khẳng định nào sau đây là đúng về hàm số y 2x4 5x2 2 .
 A. Hàm số có 2 cực đại và 1 cực tiểu.B. Hàm số có 2 cực tiểu và 1 cực đại.
 C. Hàm số không có cực trị.D. Hàm số có đúng một điểm cực trị.
 x 2
 Câu 6. Sô tt của (H):y = vuông góc với (d):y = x là ?
 x 1
 A. 0 B. 1 C. 2 D. 3
 Câu 7: Đồ thi hàm số y ax3 bx2 x 3 có tâm đối xứng là I ( -2 ; 1) khi :
 3 1 3 1 3 1 3
 A. a & b 1 B. a & b C. a & b D. a & b 
 2 4 2 4 2 4 2
 x2 7x 10
 Câu 8 : Số đường tiệm cân của đồ thi hàm số y là :
 (x 2)(x 3)
 A. 4 B. 3 C. 2 D. 1 
 e x
 Câu 9 : Cho hàm số y có đạo hàm f , (1) là : 
 x 2
 A . e2 B . –e C. 4e D .6e
 2 ,
 Câu 10 : Cho hàm số y log2 (x 1) có đạo hàm f (1) là :
 1
 A . B . 1+ln2 C .2 D .4ln2
 ln 2
 Câu 11 : Nghiệm của phương trình 43x 2 16 là :
 A .x = 3/4 B . x = 4/3 C .x = 3 D .x = 5
 Câu 12 : Tập nghiệm của phương trình lg(x 2 6x 7) lg(x 3) là:
 A . 5 B . 3;4 C . 4;8 D . Vô nghiệm
 log ( x 4 )
 Câu 13 : Tập nghiệm của bất phương trình x 2 32 là :
 1 1 1 1 
 A . ;2 B . ;4 C . ;2 D . ;4
 10 32 32 10 
 x x
 Câu 14 : Bất phương trình log2 (2 1) log3 (4 2) 2 có tập nghiệm là :
 A . ( ;0) B . (2;3) C . ;0 ] D . (0; )
 x
 Câu 15 : Bất phương trình log x log9 (3 9) 1 có nghiệm là :
 1     
A . n1 (3; 2;5) B. n2 (0;3;2) C. n3 (0;3; 2) D. n4 (0; 3; 2) .
 x 1 y 2 1 z
Câu 31 : Trong không gian oxyz, đường thẳng : có véc tơ chỉ phương là.
    3 4 5  
A.u1 (3; 4;5) B.u2 (3; 4; 5) C.u3 (3;4;5) D. u4 ( 3;4;5) 
Câu 32 : Trong không gian oxyz ,cho hai điểm A(3;2;1) và B(1;1;0).Viết phương trình 
mặt phẳng (P) đi qua B và vuông góc với đường thẳng AB.
A. 2x+y+z-3=0 B. 2x+y+z-6=0 C.4x+3y+x-7=0 D.4x+3y+x-26=0
Câu 33 : Trong không gian oxyz, cho mặt phẳng (P) : 2x + y +2z +1 = 0; 
 x 2 t
điểm A (0;1;1); đường thẳng : y 1 2t . Viết phương trình đường thẳng d qua A, d song song 
 z 3 t
với (P) và d cắt 
 x 1 y 3 z 2 x 1 y 3 z 2
A. d : B. d : C.
 1 4 1 1 4 1
 x 1 y 3 z 2 x 1 y 3 z 2
d : D. d : 
 1 4 1 1 4 1
Câu 34 : Trong không gian oxyz; cho mặt cầu (S) có tâm I(1;1;2) và mặt phẳng (P): 
2x+y+2z+2=0.Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính 
bằng 1.Viết phương trình mặt cầu (S). 
 A.(S): x 1 2 y 1 2 z 2 2 10 B.(S) : x 1 2 y 1 2 z 2 2 8 
 C. (S) : x 1 2 y 1 2 z 2 2 10 D. (S) : x 1 2 y 1 2 z 2 2 8
Câu 35 : Trong không gian oxyz, phương trình mặt cầu (S) có tâm I(2;1;-4) và tiếp xúc
 mặt phẳng ( ) : x 2y 2z 7 0 là:
A. (S) : x2 y2 z2 4x 2y 8z 4 0 B. (S) : x2 y2 z2 4x 2y 8z 4 0 .
C. S) : x2 y2 z2 4x 2y 8z 4 0 D. (S) : x2 y2 z2 4x 2y 8z 4 0
Câu 36 : Nghiệm của phương trình: là:
 7 
A. B.x k2 ; x k2 
 6 6 
C. D. 
Câu 37 : Số nghiệm của phương trình : trên là: 
 A. 2 B. 3 C. 4 D. 5
Câu 38 : Tổng tất cả các nghiệm thuộc [0; π] của phương trình :
 là:
 A. 0 B. π/2 C. π D. –π/2
Câu 39 : Trong một cuộc thi tìm hiểu về đất nước Việt Nam, ban tổ chức công bố danh 
sách các đề tài bao gồm: 8 đề tài về lịch sử, 7 đề tài về thiên nhiên, 10 đề tài về con người và 6 
đề tài về văn hóa. Mỗi thí sinh được quyền chọn một đề tài. Hỏi mỗi thí sinh có bao nhiêu khả
 năng lựa chọn đề tài ?
A. 20 B. 3360 C. 31 D. 30
Câu 40 : Trong kỳ thi THPT quốc gia năm 2016 có môn thi bắt buộc là môn Tiếng
 Anh. Môn này thi dưới hình thức trắc nghiệm với 4 phương án trả lời A, B, C, D. Mỗi câu
 trả lời đúng được cộng 0,2 điểm và mỗi câu trả lời sai bị trừ đi 0,1 điểm. bạn Hoa vì học 
rất kém môn Tiếng Anh nên chọn ngẫu nhiên cả 50 câu trả lời. Tính xác suất để bạn hoa đạt 
được 4 điểm môn Tiếng Anh trong kỳ thi trên.
 C30 3 20 A30 3 20 C30 3 20 A30 3 20
A. 50 B. 50 C. 50 D. 50
 450 450 50 50
 3 ĐÁP ÁN
 1. C 2. A 3. B 4. C 5. A 6. C 7. D 8. C 9. B 10. A
 11. B 12. A 13. C 14. C 15. C 16. C 17. D 18. B 19. B 20. C
 21. B 22. D 23. B 24. D 25. C 26. D 27. B 28. A 29. B 30. C
 31. B 32. A 33. D 34. A 35. D 36. D 37. C 38. C 39. C 40. A
 41. B 42. A 43. D 44. A 45. A 46. A 47. B 48. A 49. B 50. D
 ĐÁP ÁN CHI TIẾT
Câu 1 :ta có y’ = 3x2+ 3 > 0 với mọi x . Chọn C
Câu 2: ta có y’ = -3x2 -2mx +4m +9 . nên m2 +12m +27 
 Do đó : -9 m -3 . Có 7 gt m nguyên chọn A
Câu 3: ta có y’ = 3x2 - 6mx + 3(2m-1) .Để có CĐ và CT thì y’ = 0 có 2 ng pb nên > 0 nên
(m-1)2 > 0 khi m 1 .Chọn B
Câu 4: gpt x2+6x = -9 có ng x = -3 khi đó y = 16 . Chọn :C
Câu 5: a và b trái dấu nên loại:C và D . Hệ số a <0 nên đồ thị có 2 CĐ và 1 CT
 Chọn :A
Câu 6: gpt = -1 pt có 2 nghiệm khác 1 nên có 2 tt . Chọn : C.
Câu 7: thay x = -2 y = 1 vào hs ta có: 2a – b = 1.(1)
 y’’ = 6ax + 2b = 0 khi x = - = -2 ta có : 6a – b = 0 (2) 
 1 3
Từ đó ta có : a & b Chọn : D
 4 2
 x2 7x 10
Câu 8 : lim 1 nên y = 1 là TCN
 x (x 2)(x 3)
 x2 7x 10 x2 7x 10
 lim 0.6 ; lim 0.6
 x 2 (x 2)(x 3) x 2 (x 2)(x 3)
 x2 7x 10
 lim nên x = 3 là TCĐ
 x 3 (x 2)(x 3)
Vậy dồ thị có 2 đường tiệm cận . Chọn đáp án C
Phương án nhiễu là 3 . Vì HS nhầm TCĐ là x = 2 .
 ,
 e x e x x 2 
Câu 9. y , f , 1 e .Từ đó chọn B.
 2 3 
 x x
 2x 1
Câu 10 . f (x) log x 2 1 f , x f , 1 .Vì thế chọn A
 2 x 2 1 ln 2 ln 2
 4
Câu 11. Ta có 43x 2 16 26x 4 24 x . Từ đó chọn B
 3
 x 3
 x 3 
 lg x 2 6 x 7 lg x 3 x 5
 Câu 12. 2 x 2 
 x 6 x 7 x 3 
 x 5
 Vì thế chọn A
 log ( x 4 ) x 0
 Câu 13 . x 2 32 
 log 2 ( x ) 4 log 2 x log 2 32
 5 1 1
 h.S h'.A'B'
 V V A'B'C 1
 S.A'B'C C.SA'B' 3 2 
 V V 1 1 4 . Chọn đáp án C
 S.ABC C.SAB h.S .2h'.2AB
 3 SAB 2
Câu 26 :
Giả sử lăng trụ tam giác đều có cạnh bằng a.Khi đó
 1 3 3
V B.h .a.a. .a a3 
 2 2 4 . Chọn đáp án D
Câu 27 :
 1
 .S A'B'C'D'.h
 VO.A'B'C'D' 3 1
 . Chọn đáp án B
 VABCD.A'B'C'D' S ABCD.h 3
Câu 28 : D
 Từ giả thiết h = OO¢= 2 7 
 O'
 suy ra OI = 7, IH = 4 Þ OH = 3
 C
 HB = 4 Þ r = OB = 5 I
 Þ V = pr 2h = p.52.2 7 = 50 7p A
 Đáp án: A O H
 Câu 29 :Ta có: SA ^ (ABC) 
 Þ BC ^ SA;BC ^ AB Þ BC ^ SB B
 Þ A;B;C;S cùng nằm trên mặt cầu có đường kính SC ; 
 1 1
 bán kính R = SC = SA2 + AB 2 + BC 2 = a 2
 2 2
 Đáp án: B
Câu 30 :  
Mặt phẳng (P) : 0x + 3y - 2z + 5 = 0 có véc tơ pháp tuyến n3 (0;3; 2) , Chọn C
Câu 31 : 
 x 1 y 2 z 1
Viết lại đường thẳng : nên đường thẳng có véc tơ chỉ phương là
  3 4 5
u2 (3; 4; 5) , Chọn B
Câu 32 :  
 Mặt phẳng (P) nhận BA (2;1;1) làm véc tơ pháp tuyến.Do đó (P) : 2x y z D 0
 B(1;1;0) (P) nên D = - 3. Vậy (P) : 2x + y + z - 3= 0 . Chọn A
Câu 33 :  
 d  B(2 t; 1 2t;3 t) .Ta có AB (2 t; 2 2t;3 t) và (P) có véc tơ pháp tuyến 
      
 np (2;1;2) . Do d P(P) nên AB  np AB.np 0 t 1.Vậy B(!;-3;2) và d nhận
  x 1 y 3 z 2
 AB (1; 4;1) chỉ phương . Do đó d : . Chọn D
 1 4 1
Câu 34 : 
 Kẻ IH  (P) .Ta có IH d I;(P) 3. Đường tròn có r=1;(S) có bán kính R và 
 R r 2 IH 2 12 32 10 .Vậy (S) : x 1 2 y 1 2 z 2 2 10 . Chọn A
Câu 35 : 
 (S) tiếp xúc ( ) nên R d I;( ) 5 nên (S) : x 2 2 (y 1)2 z 4 2 25 .
Hay (S): (S) : x2 y2 z2 4x 2y 8z 4 0. Chọn D
Câu 36 : 
 7