Đề thi minh họa THPT Quốc gia năm 2020 môn Toán - Trường THPT Lê Thành Phương (Có đáp án)

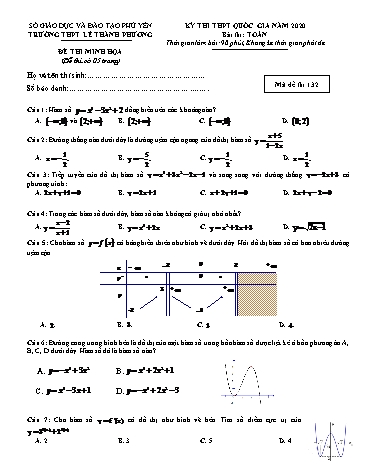
 SỞ GIÁO DỤC VÀ ĐÀO TẠO PHÚ YÊN KỲ THI THPT QUỐC GIA NĂM 2020
TRƯỜNG THPT LÊ THÀNH PHƯƠNG Bài thi: TOÁN
 Thời gian làm bài: 90 phút, Không kể thời gian phát đề
 ĐỀ THI MINH HỌA
 (Đề thi có 05 trang)
Họ và tên thí sinh:.
Số báo danh:... Mã đề thi 132
Câu 1: Hàm số y x3 3x2 2 đồng biến trên các khoảng nào?
 A. ;0 và 2; B. 2; C. ;0 D. 0;2
 . . . .
 x 5
Câu 2: Đường thẳng nào dưới đây là đường tiệm cận ngang của đồ thị hàm số y .
 1 2x
 1 5 1 1
 A. x . B. y . C. y . D. x .
 2 2 2 2
Câu 3: Tiếp tuyến của đồ thị hàm số y x3 3x2 2x 1 và song song với đường thẳng y 2x 3 có 
phương trình:
 A. 2x y 1 0 .B. y 2x 1. C. x 2y 1 0 .D. 2x y 2 0 .
Câu 4: Trong các hàm số dưới đây, hàm số nào không có giá trị nhỏ nhất?
 x 2
 A. y . B. y x4 2x . C. y x2 2x 3 . D. y 2x 1 .
 x 1
Câu 5: Cho hàm số y f x có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị hàm số có bao nhiêu đường 
tiệm cận.
 0
 x 2 2 + 
 y' + 0 +
 3 + + 
 y
 -2 2
 A. 2 . B. 3 . C. 1. D. 4 .
Câu 6: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, 
B, C, D dưới đây. Hàm số đó là hàm số nào?
 A. y x3 3x2 B. y x4 2x2 1
 C. y x3 3x 1 D. y x4 2x2 3
Câu 7: Cho hàm số y f '(x) có đồ thị như hình vẽ bên. Tìm số điểm cực trị của 
y 3f (x) 2f (x) .
 A. 2. B. 3. C. 5. D. 4. x
Câu 19: Thể tích khối tròn xoay tạo được do hình phẳng giới hạn bởi các đường y ; y 0;x 1;x 4 quay 
 4
quanh trục Ox là:
 21 21 15 15 
 A. . B. . C. .D. .
 16 16 16 8
 1
Câu 20: Cho hàm số f x . Nếu F(x) là một nguyên hàm của hàm số f(x) và đồ thị hàm số F(x) đi qua 
 sin2 x
điểm M ;0 thì F(x) là:
 6 
 3 3
 A. cot x . B. cot x . C. 3 cot x .D. 3 cot x .
 3 3
 1 1 1
Câu 21: Cho f x dx 2 và g x dx 5 khi đó f x 2g x dx bằng
 0 0 0
 A. 3 . B. 12. C. 8 . D. 1.
 1 1
Câu 22: Biết rằng x cos 2xdx a sin 2 bcos 2 c , với a,b,c ¢ . Khẳng định nào sau đây là khẳng định 
 0 4
đúng?
 A. a b c 1. B. a b c 0. C. 2a b c 1. D. a 2b c 1.
 2
Câu 23: Tính tích phân I 2x x2 1dx bằng cách đặt u x2 1, mệnh đề nào dưới đây đúng?
 1
 3 2 3 1 2
 A. I 2 udu . B. I udu . C. I udu .D. I udu .
 0 1 0 2 1
Câu 24: Cho H là hình phẳng giới hạn bởi y x , y x 2 và trục hoành. Diện tích của hình H bằng:
 10 16 7 8
 A. . B. . C. . D. .
 3 3 3 3
Câu 25: Tìm phần thực và phần ảo của số phức z i 1.
 A. Phần thực là 1 và phần ảo là . B. Phần thực là và phần ảo là 1.
 C. Phần thực là 1 và phần ảo là i. D. Phần thực là i. và phần ảo là 1.
Câu 26: Gọi M, N, P lần lượt là các điểm biểu diễn của các số phức z1 1 i, z2 8 i, z3 1 3i trong mặt 
phẳng phức Oxy. Khẳng định nào sau đây là khẳng định đúng?
 A. MNP cân. B. MNP đều.C. MNP vuông. D. MNP vuông cân.
Câu 27: Cho số phức z1 3 2i,z2 6 5i . Tìm số phức liên hợp của số phức z 6z1 5z2 .
 A. z 51 40i . B. z 51 40i . C. z 48 37i . D. z 48 37i .
 z i
Câu 28: Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn số phức z thỏa mãn 1.
 z i
 A. Hai đường thẳng y 1, trừ điểm 0; 1 .
 B. Hình chữ nhật giới hạn bởi các đường x 1, y 1.
 C. Đường tròn x 1 2 y 1 2 1.
 D.Trục Ox. Câu 41: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Lấy điểm M trên đoạn SD thỏa MS 
= 2MD. Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng:
 1 5 3 1
 A. . B. . C. . D. .
 3 5 3 5
Câu 42: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng 
(ABC) và góc giữa đường thẳng SB với mặt phẳng đáy bằng 60. Khoảng cách giữa hai đường thẳng AC và 
SB bằng:
 a 2 a 15 a 7
 A. . B. . C. 2a. D. .
 2 5 7
Câu 43: Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P) : 2x y 3z 1 0 có một vectơ pháp tuyến 
là:     
 A. n1 2; 1;3 . B. n2 2; 1; 1 . C. n3 1;3; 1 . D. n4 2; 1; 3 .
Câu 44: Trong không gian với hệ trục tọa độ Oxyz, phương trình đường thẳng đi qua điểm A 1; 2;3 và có 
vectơ chỉ phương u 2; 1; 2 là:
 x 1 y 2 z 3 x 1 y 2 z 3 x 1 y 2 z 3 x 1 y 2 z 3
 A. . B. . C. . D. .
 4 2 4 2 1 2 2 1 2 2 1 2
Câu 45: Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(2;2; 1) và N(0; 2;5) . Viết phương trình mặt 
phẳng ( ) là mặt trung trực của đoạn thẳng MN .
 A. ( ) : x 2y 3z 10 0 . B. ( ) : x 2y 3z 5 0 .
 C. ( ) : 2x 2y z 9 0 . D. ( ) : 2y 5z 9 0 .
Câu 46: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(2; 1; -2) và B(4; 3; 2). Viết phương trình 
mặt cầu (S) nhận đoạn AB làm đường kính.
 A. (S) : (x 3)2 (y 2)2 z2 24. B. (S) : (x 3)2 (y 2)2 z2 6.
 C. (S) : (x 3)2 (y 2)2 z2 24. D. (S) : (x 3)2 (y 2)2 z2 6.
 x 1 y 2 z 1
Câu 47: Trong không gian với hệ trục tọa độ Oxyz, tìm tọa độ điểm H trên đường thẳng d : 
 1 1 2
sao cho độ dài đoạn MH là ngắn nhất, biết rằng điểm M(2; 1; 4).
 A. H(1; 3; 3). B. H(2; 2; 3). C. H(2; 3; 4). D. H(2; 3; 3).
Câu 48: Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu S : x2 y2 z2 4x 6y m 0 và đường 
thẳng là giao tuyến của hai mặt phẳng : x 2y 2z 4 0 và  : 2x 2y z 1 0. Đường thẳng 
cắt mặt cầu S tại hai điểm phân biệt A,B thỏa mãn AB 8 khi:
 A. m 12. B. m 12. C. m 10. D. m 5.
Câu 49: Trong không gian với hệ trục tọa độ Oxyz, cho A(0; -2; 2 – m), B(m + 3; -1; 1), C(-4; -3; 0), D(-1; -2; 
m – 1). Tập hợp các giá trị của m để bốn điểm A, B, C, D đồng phẳng là tập con của tập hợp nào sau đây?
 A. (-7; -2). B. (3; 6). C. (5; 8). D. (-2; 2).
Câu 50: Trong không gian, cho tam giác ABC là tam giác đều có cạnh bằng 2 không đổi. Gọi M là một điểm 
thay đổi luôn thỏa mãn điều kiện MA2 MB2 2MC2 12 . Khẳng định nào sau đây là khẳng định đúng?
 2 7
 A. Tập hợp các điểm M là mặt cầu có R 7 . B. Tập hợp các điểm M là mặt cầu có R .
 3
 7 2 7
 C. Tập hợp các điểm M là mặt cầu có R . D. Tập hợp các điểm M là mặt cầu có R .
 2 9
 ----------- HẾT ----------