Đề minh họa kỳ thi THPT Quốc gia năm 2020 môn Toán - Trường Phổ thông Duy Tân (Có đáp án)

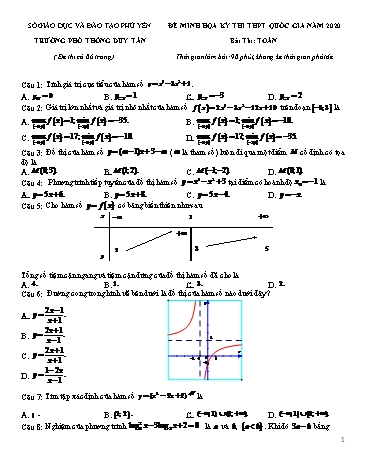
 SỞ GIÁO DỤC VÀ ĐÀO TẠO PHÚ YÊN ĐỀ MINH HỌA KỲ THI THPT QUỐC GIA NĂM 2020
 TRƯỜNG PHỔ THÔNG DUY TÂN Bài Thi: TOÁN
 ( Đề thi có 06 trang) Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1: Tính giá trị cực tiểu của hàm số y x3 3x2 1.
A. y 0 B. y 1 C. y 3 D. y 2
 CT CT CT CT
Câu 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x 2x3 3x2 12x 10 trên đoạn  3;3 là
A. max f x 1; min f x 35. B. max f x 1; min f x 10.
  3;3  3;3  3;3  3;3
C. max f x 17; min f x 10. D. max f x 17; min f x 35.
  3;3  3;3  3;3  3;3
Câu 3: Đồ thị của hàm số y (m 1)x 3 m ( m là tham số) luôn đi qua một điểm M cố định có tọa 
độ là 
A. M (0;3). B. M (1;2). C. M ( 1; 2). D. M (0;1).
 3 2
Câu 4: Phương trình tiếp tuyến của đồ thị hàm số y x x 3 tại điểm có hoành độ x0 1 là
A. y 5x 6. B. y 5x 8. C. y 5x 4. D. y x.
Câu 5: Cho hàm số y f x có bảng biến thiên như sau
 x 1 
 2 3 5
 y
 3
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A. 4. B. 12. C. 3. D. 2.
Câu 6: Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào dưới đây?
 y
 2x 1
A. y .
 x 1
 2x 1
B. y .
 x 1 2
 2x 1
C. y . x
 -2 -1 0 1
 x 1 -1
 1 2x
D. y .
 x 1
Câu 7: Tìm tập xác định của hàm số y (x2 3x 2) 17 là
A. ¡ . B. 1; 2 . C. ( ;1)  (2; ). D. ( ;1][2; ).
 2
Câu 8: Nghiệm của phương trình log3 x 3log3 x 2 0 là a và b , a b . Khi đó 3a b bằng
 1 A. n 20. B. n 21. C. n 22. D. n 23.
Câu 19: Cho hình chóp S.ABC có SA  ABC , đáy ABC là tam giác đều. Tính thể tích khối chóp 
S.ABC biết AB a , SA a.
 a3 3 a3 3 C. a3. a3
A. . B. . D. .
 12 4 3
Câu 20: Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a . 
Tính diện tích xung quanh của hình nón.
 a2 2 a2 2 C. a2 2. 2 a2 2
A. . B. . D. .
 4 2 3
Câu 21: Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6 (cm) và thiết diện đi qua 
trục là một hình chữ nhật có độ dài đường chéo bằng 10 (cm) .
 3 3 3 3
A. 48 (cm ). B. 24 (cm ). C. 72 (cm ). D. 18 (cm ).
Câu 22: Trong không gian Oxyz , phương trình nào sau đây là phương trình tham số của đường thẳng 
d qua điểm M 2;3;1 và có vectơ chỉ phương a 1; 2;2 ? 
 x 2 t x 1 2t x 1 2t x 2 t
A. y 3 2t. B. y 2 3t. C. y 2 3t. D. y 3 2t .
 z 1 2t z 2 t z 2 t z 1 2t
Câu 23: Cho hai điểm A 1;0; 3 và B 3;2;1 . Phương trình mặt cầu đường kính AB là
A. x2 y2 z2 4x 2y 2z 0. B. x2 y2 z2 4x 2y 2z 0.
 2 2 2 2 2 2
C. x y z 2x y z 6 0. D. x y z 4x 2y 2z 6 0.
Câu 24: Trong không gian với hệ toạ độ Oxyz . Điểm nào sau đây không thuộc mặt phẳng 
 P : 2x y 5 0
A. ( 2;1;0). B. ( 2;1; 5). C. (1;7;5). D. ( 2;2; 5).
Câu 25: Trong không gian Oxyz , cho hai mặt phẳng P : 2x my 2mz 9 0 và 
 Q : 6x y z 10 0 . Tìm m để P  Q .
A. m 4. B. m 4. C. m 2. D. m 2.
[]
 x 2 t x 1 t
Câu 26: Cho hai đường thẳng d1 : y 1 t và d2 : y 2 . Góc giữa hai đường thẳng d1 và 
 z 3 z 2 t
d2 là
A. 30o. B. 120o. C. 150o. D. 60o.
 8
 3 1 
Câu 27: Số hạng không chứa x trong khai triển: x là
 x 
 3 A. m 8. B. m 2. 13 5
 C. m . D. m .
 2 2
 1 1
Câu 36: Cho hai số thực a, b đều lớn hơn 1.Giá trị nhỏ nhất của biểu thức S là
 log a log b
 ab 4 ab
 4 9 9 1
A. . B. . C. . D. .
 9 4 2 4
Câu 37: Tìm số phức z sao cho 1 2i z là số thuần ảo và 2z z 13 
A. z 2 i hoặc z 2 i. B. z 2 i hoặc z 2 i.
C. z 2 i hoặc z 2 i. D. z 2 i hoặc z 2 i.
Câu 38: Cho phương trình z2 mz 2m 1 0 trong đó m là tham số phức. Giá trị của m để phương 
 2 2
trình có hai nghiệm z1, z2 thỏa mãn z1 z2 10 là
A. m 2 2 2i. B. m 2 2 2i. C. m 2 2 2i. D. m 2 2 2i.
Câu 39: Sự tăng trưởng của một loài vi khuẩn tuân theo công thức N A.ert , trong đó A là số lượng vi 
khuẩn ban đầu, r là tỉ lệ tăng trưởng r 0 và t là thời gian tăng trưởng. Biết số lượng vi khuẩn ban 
đầu có 250 con và sau 12 giờ là 1500 con. Hỏi sau bao lâu thì số lượng vi khuẩn tăng gấp 216 lần số 
lượng vi khuẩn ban đầu?
A. 48 giờ. B. 24 giờ. C. 60 giờ. D. 36 giờ.
Câu 40: Cho hình chóp S.ABCD có SA  ABCD , đáy ABCD là hình chữ nhật với AC a 5 và 
BC a 2 . Tính khoảng cách giữa SD và BC. 
 2a a 3 3a D. a 3.
A. . B. . C. .
 3 2 4
 2
 3 x 8 b b 
Câu 41: Biết dx 3ln a 4ln thì bằng
 2 
 0 x 5x 4 a a 
 7 16 49 1
A. . B. . C. . D. .
 4 49 16  16  
Câu 42: Cho hình lập phương ABCD.EFGH . Hãy xác định góc giữa hai vectơ AB và EG ?
A. 45o. B. 60o. C. 90o. D. 120o.
Câu 43: Cho khối lăng trụ ABC.A B C , mặt bên ABB A có diện tích bằng 10. Khoảng cách đỉnh C 
đến mặt phẳng ABB A bằng 6 . Thể tích khối lăng trụ đã cho bằng
A. 40. B. 60. C. 30. D. 20.
 0
Câu 44: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 3a .Các mặt bên tạo với đáy một góc60 . 
Tính thể tích V mặt cầu ngoại tiếp hình chóp S.ABC .
 5