Đề cương ôn tập học kỳ II môn Toán 12 - Năm học 2018-2019 - Trường THCS-THPT Võ Nguyên Giáp

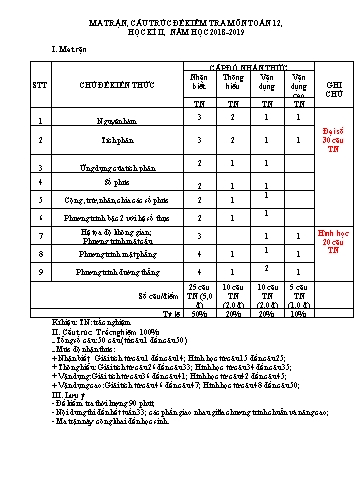
 MA TRẬN, CẤU TRÚC ĐỀ KIỂM TRA MÔN TOÁN 12, 
 HỌC KÌ II, NĂM HỌC 2018-2019
 I. Ma trận 
 CẤP ĐỘ NHẬN THỨC
 Nhận Thông Vận Vận 
STT CHỦ ĐỀ KIẾN THỨC biết hiểu dụng dụng GHI 
 cao CHÚ
 TN TN TN TN
 3 2 1 1
 1 Nguyên hàm
 Đại số
 2 Tích phân 3 2 1 1 30 câu 
 TN
 2 1 1
 3 Ứng dụng của tích phân
 4 Số phức
 2 1 1
 1
 5 Cộng ,trừ ,nhân ,chia các số phức 2 1
 1
 6 Phương trình bậc 2 với hệ số thực 2 1
 Hệ tọa độ không gian ; Hình học
 7 3 1 1
 Phương trình mặt cầu 20 câu 
 1 TN
 8 Phương trình mặt phẳng 4 1 1
 2
 9 Phương trình đường thẳng 4 1 1
 25 câu 10 câu 10 câu 5 câu 
 Số câu/điểm TN (5,0 TN TN TN
 đ) (2,0 đ) (2,0 đ) (1,0 đ)
 Tỷ lệ 50% 20% 20% 10%
 Kí hiệu: TN: trắc nghiệm 
 II. Cấu trúc: Trắc nghiệm 100%
 - Tổng số câu: 50 câu (từ câu 1 đến câu 50)
 - Mức độ nhận thức: 
 + Nhận biết: Giải tích từ câu 1 đến câu 14; Hình học từ câu 15 đến câu 25;
 + Thông hiểu: Giải tích từ câu 26 đến câu 33; Hình học từ câu 34 đến câu 35;
 + Vận dụng: Giải tích từ câu 36 đến câu 41; Hình học từ câu 42 đến câu 45; 
 + Vận dụng cao: Giải tích từ câu 46 đến câu 47; Hình học từ câu 48 đến câu 50;
 III. Lưu ý
 - Đề kiểm tra thời lượng 90 phút;
 - Nội dung thi đến hết tuần 33; các phần giao nhau giữa chương trình chuẩn và nâng cao;
 - Ma trận này công khai đến học sinh. 
Câu 10. Biết F x là một nguyên hàm của hàm số f x sin 2x.cos x và F 0 . Tính 
 3 
F . 
 2 
 1 7 3 11
 A. F B. F C. F . D. F . 
 2 12 2 12 2 4 2 12
Câu 11. Cho hàm số f x x.sin x x2 . Tìm nguyên hàm G(x) của hàm số g x x.cos x , biết 
rằng G 0.
 A. G x sinx C. B. G x x.sinx cos x 1.
 C. G x x.sinx cos x C. D. G x x.cosx sin x 1.
Câu 12. Cho hàm số f x x.cosx x2 . Tìm nguyên hàm G(x) của hàm số g x x.sin x , biết 
rằng G 3.
 2 
 A. G x sinx-x.cos x 2. B. G x cos x C.
 C. G x sinx-x.cos x. D. G x cosx-x.sin x 2.
Câu 13. Cho hàm số f x x ln x x2 , x>0 . Tìm nguyên hàm G(x) của hàm số g x ln x , 
biết rằng G 2 2.
 A. G x x ln x x C. B. G x x ln x x 2ln 2.
 1
 C. G x C. D. G x x ln x x 2ln 2.
 x
Câu 14. Cho hàm số f x x 3 ex , F x ax2 bx c ex , a,b,c ¢ .. Tìm a, b, c đề hàm 
số F x là một nguyên hàm của hàm số f x .
 A. a 0, b=1, c=-4 . B. a 1, b=0, c=-4 .
 C. a 0, b=-4, c=1. D. a 0, b=1, c=-3. 
 2/ TÍCH PHÂN
Câu 15. Tính tích phân I 6 sin 3xdx . 
 0
 1 
 A. I . B. I 1. C. I . D. I .
 3 6 3
Câu 16. Cho hàm số f x có đạo hàm trên đoạn [0;3], f 0 3 và f 3 9. Tính 
 3
I f ' x dx . 
 0
 A. I=-6. B. I=12. C. I=6. D. I=3. 
Câu 17. Cho hàm số f x có đạo hàm trên đoạn [0; ], f 0 2 . Biết I f ' x dx 5 . 
 0
Tính f .
 A. f 7 . B. f 3 . C. f 3 . D. 
 f 2 . . 
 4 2
Câu 18. Cho f x dx 10 . Tính I f 2x dx.
 0 0
 A. I=5. B. I=20. C. I=10. D. I=40. 
 18 6
Câu 19. Cho f x dx 27 . Tính I f 3x dx.
 3 1
 A. I=9. B. I=81. C. I=10. D. I=15. 
 8 16 x 
Câu 20. Cho f x dx 24 . Tính I f dx.
 2 4 2 Câu 33. Tìm diện tích của hình phẳng được giới hạn bởi hai đồ thị hàm số có phương trình 
y x 1 ln x, y=x-1.
 e2 5 e2 5 e2 5 e2 5
 A. e B. e C. e D. e .
 4 4 4 4 4 4 4 4
Câu 34. Tìm diện tích của hình phẳng được giới hạn bởi hai đồ thị hàm số có phương trình 
y x 1 ex , y=x-1.
 5 5 2
 A. e B. e C. e 5 D. e .
 2 2 5
Câu 35. Cho hình phẳng (H) giới hạn bởi các đường y x ln x, y=0, x=e. Thể tích vật thể 
tròn xoay khi cho hình phẳng (H) quay quanh trục hoành là: 
 2 2 2
 A. e2 1 B. e2 1 C. e 1 D. e2 1 .
 4 4 4 4
Câu 36. Nếu gọi S là diện tích hình phẳng giới hạn bởi các đường x =0, x = 3, y = 0, y = x - 
1 thì khẳng định nào sau đây là đúng? 
 A.S = 3 B. S= 1 C. S = 2 D. S = 5 
 2 2 2
Câu 37..Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y x3 3x2 4 và đường thẳng 
x y 1 0 .
 A. 8 (đvdt).B. 4 (đvdt).C. 6 (đvdt). D. 0 (đvdt).
Câu 38. Thể tích V của khối tròn xoay khi quay hình phẳng H giới hạn bởi y x2 và 
y x 2 quanh trục Ox là
 72 81 81 72 
 A. V (đvtt).B. V (đvtt).C. V (đvtt).D. V (đvtt). 
 5 10 5 10
Câu 39. Thể tích của vật thể tròn xoay có được khi quay quanh trục Ox hình phẳng được 
giới hạn bởi parabol P : y 4 x2 , đường thẳng d : y x 2 và trục Ox là:
 A.188 B. 88 C. 8 D. 
 15 15 15 15
Câu 40. Một ca nô đang chạy trên hồ Tây với vận tốc 20 m/s thì hết xăng.Từ thời điểm đó, 
ca nô chuyển động chậm dần đều với vận tốc v(t) 20 5t(m / s) , trong đó t là khoảng thời 
gian tính bằng giây, kể từ lúc hết xăng .Hỏi từ lúc hết xăng đến lúc dừng hẳn ca nô đi được 
bao nhiêu mét?
 A.40m B. 30m C.20m D.10m
Câu 41. Một vật chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc a t 3t t 2 .Tính 
quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc.
 A. 4300 m B. 430 m C.4300m D.430m
 3 3
II.SỐ PHỨC:
Câu 1. Cho số phức z 5 3i . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn 
số phức w iz ?
 A. A1 3;5 . B. A2 3;5 . C. A3 3; 5 . D. 9;5 . 
Câu 2. Cho số phức z 4 5i . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn 
số phức w iz 1?
 A. A1 6;4 . B. A2 4;4 . C. A3 24;4 . D. 4;6 . 
 2
Câu 3. Kí hiệu z1 , z2 là hai nghiệm phức của phương trình z 4z 5 0 . Tính z1.z2 . 
 A. z1.z2 3. B. z1.z2 5. C. z1.z2 4. D. z1.z2 10.
 2
Câu 4. Kí hiệu z1 , z2 là hai nghiệm phức của phương trình z 2z 10 0 . Tính z1.z2 . C. Phần thực là -1, phần ảo là 2D. Phần thực là -1, phần ảo là -2. 
 2
Câu 21. Phần thực và phần ảo của số phức z thỏa mãn z 2 i 1 i 2 là: 
 A. Phần thực là 5, phần ảo là 2 B. Phần thực là 5, phần ảo là 2
 C. Phần thực là -5, phần ảo là 2 D. Phần thực là -5, phần ảo là i 2
Câu 22. Phần thực và phần ảo của số phức z thỏa mãn 1 2i z 3 i 1 i z là: 
 7 7
 A. Phần thực là , phần ảo là -3B. Phần thực là , phần ảo là 3.
 3 3
 7 7
 C. Phần thực là , phần ảo là 2D. Phần thực là , phần ảo là -3. 
 3 3
Câu 23. Mô đun của số phức z thỏa mãn 1 i z 2 i z 4 i là: 
 A. 5 B. 5 C. 52 D. 3 . 
Câu 24. Mô đun của số phức z thỏa mãn 3 i z 1 i 2 i 5 i là: 
 A. 2 B. 2 5 C. 5 D. 2 5 . 
 5 5 5 25
Câu 25. Cho số phức z thỏa mãn 2 i z 4 3i Mô đun của số phức w iz 2z là: 
 A. 41 B. 5 C. 5 D. 14 . 
Câu 26. Mô đun của số phức z thỏa mãn 1 2i z 4 3i 2 i 2 là: 
 A. 10 B. 9 C. 50 D. 49 . 
 9 7i
Câu 27. Mô đun của số phức z thỏa mãn 1 2i z 5 2i là: 
 3 i
 A. 13 B. 17 C. 8 D. 10 . 
 2 3i
Câu 28. Mô đun của số phức z thỏa mãn z 2 i 1 2i là: 
 1 i
 170
 A. 170 B. C. 17 D. 9. 
 2
Câu 29. Cho số phức z thỏa mãn 3 z 1 i 2i z 2 . Mô đun của số phức w z iz 5 là: 
 A. 10 B. 5 C. 10 5 D. 25. 
 2
Câu 30. Gọi z1 , z2 là hai nghiệm phức của phương trình z 6z 13 0. Giá trị biểu thức 
z1 z2 là: 
 A. 4 B. 0 C. 26 D. 13
III.HÌNH HỌC:
Câu 1. Khoảng cách từ điểm M(-1;-3;-2) đến mặt phẳng (P): x y z 3 0 là: 
 3
 A. 3 B. C. 2 3 D. 3 2 .
 2
Câu 2. Cho ba điểm A(2;1;0), B(0;3;4), C(5;6;7). Khoảng cách từ điểm C đến mặt phẳng 
trung trực của đoạn thẳng AB là: 
 A. 5 5 B. 5 6 C. 5 3 D. 6 .
 3 3 3 3
Câu 3. Côsin của góc giữa mặt phẳng (P): 2x-y-2=0 và mặt phẳng (Oxz) bằng: 
 5 1 1
 A. B. 5 C. D. .
 5 5 5
Câu 4. Cho A(1;3;-2) và (P): 2x-y+2z-1=0. Mặt cầu tâm A và tiếp xúc với (P) có phương 
trình là: 
 A. x 1 2 y 3 2 z 2 2 4 B. x 1 2 y 3 2 z 2 2 2 A. 0;2;3 B. 1;3;2 C. 2;4;1 D. 3; 1;6 .
Câu 16. Giao điểm của đường thẳng AB và mặt phẳng (P): x-2y+2z-5=0 với A(1;-1;2), 
B(3;0;-4) là: 
 4 5 4 5 4 5 4 5 
 A. ; ; 1 B. ; ;1 C. ; ;1 D. ; ;1 .
 3 6 3 6 3 6 3 6 
Câu 17. Cho A(1;1;2), B(2;-1;0). Phương trình mặt phẳng đi qua điểm A và vuông góc với 
AB là: 
 A. x 2y 2z 5 0 B. x 2y 2z 6 0
 C. x 2y 2z 3 0 D. 3x 2y 2z 5 0. 
Câu 18. Cho hai điểm A(1;-1;2), B(3;0;-4) và mặt phẳng (P): x-2y+2z-5=0. Phương trình 
mặt phẳng qua hai điểm A, B và vuông góc với (P) là: 
 A. 2x+2y+z-3=0B. -2x-2y-z-2=0C. 2x+3y+2z-2=0D. 2x+2y+z-2=0. 
Câu 19. Cho A(1;2;-1), B(3;0;-5). Phương trình mặt phẳng trung trực của đoạn thẳng AB là: 
 A. x y 2z 1 0 B. x y 2z 7 0 C. x y 2z 13 0 D. x y 2z 6 0 . 
Câu 20. Cho A(-1;1;2), B(0;1;1), C(1;0;4). Phương trình mặt phẳng qua ba điểm A, B, C là: 
 A. x 4y 2z 7 0 B. x y 4z 5 0 C. x 4y z 5 0 D. 4x y z 5 0 . 
 x 1 y 1 z
Câu 21. Cho A(1;-1;0) và d : . Phương trình mặt phẳng chứa A và d là: 
 2 1 3
 A. x 2y z 1 0 B. x y z 0 C. x y 0 D. y z 0
 x 3 y 8 z
Câu 22. Mặt phẳng chứa d : và vuông góc với (P): x+y+z-7=0 là: 
 2 4 1
 A. 5x y 6z 7 0 B. x 5y 6z 7 0 C. 5x 6y z 7 0 D. 
 6x y 5z 7 0
Câu 23. Phương trình mặt phẳng (P) song song với mặt phẳng (Q): 2x+y+2z-1=0 và 
d(A,(P))=2d(B,(P)) với A(1;-1;2), B(-2;1;3) là: 
 A. 6x 3y 6z 11 0 B. 6x 3y 6z 11 0
 C. 6x 3y 6z 10 0 D. 6x 3y 6z 12 0. 
 x 1 y 2 z 1
Câu 24. Cho A(2;-2;1), đường thẳng d : và mặt phẳng (P): x-2y-z-3=0. 
 1 2 1
Phương trình mặt phẳng qua A song song với d và vuông góc với (P) là: 
 A. y 2z 4 0 B. x 2z 4 0
 C. 2y z 3 0 D. x 2y 6 0 . 
Câu 25. Cho (S): x2 y2 z2 2x 2y 4z 3 0 và hai điểm A(1;0;1), B(-1;1;2). Phương 
trình mặt phẳng đi qua hai điểm A, B và cắt mặt cầu theo giao tuyến là một đường tròn có 
bán kính lớn nhất là: 
 A. x y z 2 0 B. x 4y 2z 1 0
 C. x 4y 2z 3 0 D. 2x 4y z 1 0 . 
Câu 26. Phương trình đường thẳng đi qua hai điểm A(5;5;0), B(4;3;1) là: 
 x 1 y 2 z 1 x 5 y 5 z
 A. B. 
 4 3 1 1 2 1
 x 4 y 3 z 1 x 4 y 3 z 1
 C. D. 
 1 2 1 1 2 1
Câu 27. Cho điểm A(2;-1;0) và mặt phẳng (P): x-2y-3z+10=0. Phương trình đường thẳng đi 
qua A và vuông góc với (P) có phương trình là: 
 x 2 y 1 z x 2 y 1 z 3
 A. B. 
 1 2 3 1 2 3