Đề cương ôn tập học kì I môn Toán Lớp 12 - Năm học 2018-2019 - Trường THCS&THPT Võ Nguyên Giáp

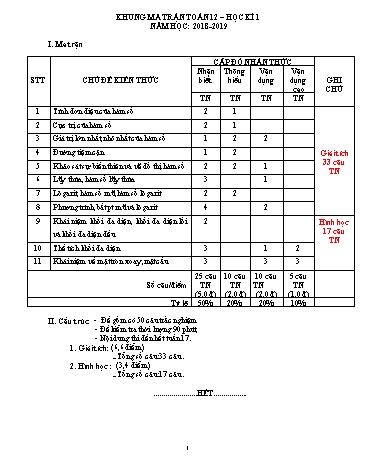
 KHUNG MA TRẬN TOÁN 12 – HỌC KÌ 1
 NĂM HỌC: 2018-2019
 I. Ma trận
 CẤP ĐỘ NHẬN THỨC
 Nhận Thông Vận Vận 
STT CHỦ ĐỀ KIẾN THỨC biết hiểu dụng dụng GHI 
 cao CHÚ
 TN TN TN TN
 1 Tính đơn điệu của hàm số 2 1
 2 Cực trị của hàm số 2 1
 3 Giá trị lớn nhất,nhỏ nhất của hàm số 1 2 2
 4 Đường tiệm cận 1 2 Giải tích
 33 câu 
 5 Khảo sát sự biến thiên và vẽ đồ thị hàm số 2 2 1
 TN
 6 Lũy thừa, hàm số lũy thừa 3 1
 7 Lôgarit, hàm số mũ,hàm số lôgarit 2 2
 8 Phương trình,bất pt mũ và lôgarit 4 2
 9 Khái niệm khối đa diện, khối đa diện lồi 2 Hình học
 17 câu 
 và khối đa diện đều
 TN
 10 Thế tích khối đa diện 3 1 2
 11 Khái niệm về mặt tròn xoay,mặt cầu 3 3 3
 25 câu 10 câu 10 câu 5 câu 
 Số câu/điểm TN TN TN TN
 (5,0 đ) (2,0 đ) (2,0 đ) (1,0 đ)
 Tỷ lệ 50% 20% 20% 10%
 II. Cấu trúc: - Đề gồm có 50 câu trắc nghiệm
 - Đề kiểm tra thời lượng 90 phút;
 - Nội dung thi đến hết tuần 17.
 1. Giải tích: (6,6 điểm)
 - Tổng số câu: 33 câu .
 2. Hình học : (3,4 điểm)
 - Tổng số câu: 17 câu .
 ......................HẾT.................
 1 + Tính y(a)=?, y(x1)=?,.,y(b)=? 
 + So sánh và kết luận : max y ? min y ?
 [a;b] [a;b]
 4) Tiệm cận (xem SGK)
 5) Sơ đồ khảo sát hàm số (SGK)
 6) Phương trình tiếp tuyến của (C ) tại điểm M0(x0;y0) (C ) là :
 y f'(x0)(x x0) y0 ( k=f’(x) là hệ số góc )
 Chương II : HÀM SỐ LŨY THỪA, HS MŨ, HS LÔGARIT
 1. Lũy thừa :
 a)Lũy thừa với số mũ nguyên : d) Tính chất lũy thừa với số mũ thực :
 1 Với a,b >0 và x,y R ta có :
 * a0 = 1 ; a n ; 00 và 0-n vô nghĩa
 a n * a x .a y a x y
 b) Tính chất căn bậc n : a x
 * a x y
 a y
 n n n
 * a. b ab y
 * a x a xy
 n a n a
 * * a.b x a x .b x
 n n 
 b b 
 x x
 m a a
 n n m * 
 * a a x
 b b
 * n k a nk a
 e)So sánh lũy thừa :
c) Lũy thừa với số mũ hữu tỉ : a 1 
 m * a a
 n m 
*a n a ( Với a > 0, n,m Z, n 2)
 1 0 a 1 
 n n * a a
* a a ( với a>0 , n Z, n 2) 
2.Hàm số lũy thừa, hs mũ. Hs lôgarít
 a)Các phép toán đạo hàm cơ bản:
*(C)’=0 ( C là hằng số ) *(u.v)' u'.v v'.u
*(u v)’=u’ v’ '
*(k.u)’ = k.(u)’ u u'.v v'.u
 * (v 0)
 v v2
 b) Đạo hàm của hs đơn giản Đạo hàm của hs hợp
 ' '
* x .x 1 * u .u 1.u'
 ' '
 1 1 1 u'
 * 2
* 2 u u
 x x 
 ' u'
 ' 1 * u 
* x 2 u
 2 x
*(ex )' ex *(eu )' u'.eu
 ' '
* ax ax.lna * au u'.au.lna
 3 b 0 Bất Phương trình vô nghiệm
 b. a f (x) b 
 f (x) f (x) loga b khi a 1
 b 0 Bất Pt : a b 
 f (x) loga b khi 0 a 1
 Biến đổi bất phương trình về dạng cùng cơ số: Bất Phương trình cơ bản(dạng2)
 f (x) g (x) f (x) g(x) khi a 1
 a. a a 
 f (x) g(x) khi 0 a 1
 f (x) g (x) f (x) g(x) khi a 1
 b. a a 
 f (x) g(x) khi 0 a 1
 Đặt ẩn phụ chuyển về bất phương trình đại số.
 Ví dụ : Giải bất phương trình: 5x 52 x 26 
 x 2 x x 25 x 2 x
 HD: 5 5 26 5 x 26 0 5 26.5 25 0 (1)
 5
 Đặt t 5x 0
 Ta có: (1) t 2 26t 25 0 1 t 25
 1 5x 25 50 5x 52 0 x 2
 Vậy bất phương trình có nghiệm: S 0;2 
6. Bất phương trình lôgarit
 Phương trình cơ bản1:
 f (x) ab khi a 1
 a. log f (x) b , Điều kiện f (x) 0
 a b
 f (x) a khi 0 a 1
 f (x) ab khi a 1
 b. log f (x) b , Điều kiện f (x) 0
 a b
 f (x) a khi 0 a 1
 Biến đổi bất phương trình về dạng cùng cơ số( Dạng cơ bản 2)
 f (x) g(x) khi a 1
 a. loga f (x) loga g(x) , Điều kiện f (x) 0, g(x) 0
 f (x) g(x) khi 0 a 1
 f (x) g(x) khi a 1
 b. loga f (x) loga g(x) , Điều kiện f (x) 0, g(x) 0
 f (x) g(x) khi 0 a 1
 Đặt ẩn phụ chuyển về bất phương trình đại số.
 2
 Ví dụ 1: Giải bất phương trình: log0,5 x log0,5 x 2
 HD: + Điều kiện: x 0
 + Đặt : t log0,5 x
 2 2 2
 + Lúc đó: log0,5 x log0,5 x 2 t t 2 t t 2 0 2 t 1
 5 4 1 2
 a 3 a 3 a 3 
 0,75 5 
 1 
 1) A (0,25) 2 2) B với a>0
 1 3 1
 16 
 4 4 4 
 a a a 
 3 1
 1 1 3 1 2 1
 a 1 a a 2 1 
3) C 2b (2b) 4) D a . 
 5 3 4 5
 2 2 a .a a 
Bài 7 : a) Cho m = log52 và n = log53. Hãy phân tích log 5 432 theo m và n
 b) Cho a= log712 và log1224 = b. Hãy phân tích log5168 theo a và b.
Bài 8 : I/ Giải các pt mũ sau:
 x 10 x 5
 x x x
1) 16 x 10 0,125.8 x 15 2) 32x 8 4.3x 5 27 0 3) 6.9 13.6 6.4 0 4)
 2 5
 x2 x 8 1 3x x 6x 
( 2 3)x ( 2 3)x 4 5) 2 4 6) 2 2 16 2 
 x x 1 x 2 x x 1 x 2
7) 2 2 2 3 3 3 8) 2x.3x 1.5x 2 12
 x x x x 1 x 2 x x 1 x 2
9) (7 4 3) 3(2 3) 2 0 10) 5 5 5 3 3 3
 II/ Giải các bất phương trình mũ sau:
 2x 5 6
 x 4 1 x
 1. 16 8 ; 2. 9 ; 3. 9 3x 2
 3 
 4x2 15x 4 4x2 15x 13 4 3x
 x2 x 6 1 3x 4 1 1 
 4. 4 1; 5. 2 ; 6. 
 2 2 2 
 x
 x2 7 x 12 x 1 1 x 2 x 2 3x 3x
 7. 5 1; 8. 2 ; 9. 2 .5 2 .5
 16 
 x 1 x2 3
 10. 25x 1 125 ; 11. 22x 6 22x 7 17 ; 12. 2 3 2 3 
 1 1
 1 2
 13. 52x 3 2.5x 2 3; 14. 4 x 2 x 3 ; 15 5.4x 2.25x 7.10x
 x 10 x 5
 16. 16 x 10 0,125.8 x 15 ; 17. 32x 8 4.3x 5 27 0 ; 18. 6.9x 13.6x 6.4x 0 
 III/ Giải các phương trình logarit sau
 4x 6
 1. log x 2.log2x 2.log2 4x 1 ; 2. log1 0
 3 x
 3. log2 x 3 1 log2 x 1 ; 4. log3 log 1 x 0
 2 
 2
 5. 2log (x 2) log (x 3) ; 6. log (4x 4) x log (2x 1 3) 
 8 1 3 2 1
 8 2
 1 2
 7. log 2 (x 1) log 1 (x 4) log 2 (3 x)
 2 2
 8. log5 x log5 x 6 log5 x 2 
 IV/Giải các bất phương trìnhlogarit sau:
 7